この著作で定義されている通りです。 は、次数のホイールグラフであり、単にホイールと呼ばれることもある（Harary 1994, p. 46; Pemmaraju and Skiena 2003, p.248; Tutte 2005, p.78）、次数のサイクルを含み、サイクルの全てのグラフ頂点がハブと呼ばれる他のグラフ頂点に接続されているグラフである。 ハブを含む輪の辺をスポークと呼ぶ(Skiena 1990, p. 146)。 車輪はグラフ結合として定義でき、はシングルトングラフ、はサイクルグラフで、-コーングラフとなる。

なお、車輪グラフのインデックス付けには2通りの慣例があり、著者によっては（例えば,

四面体グラフ（つまり）はに、は完全三面体グラフに同型であることに注意してほしい。 一般に輪グラフはピラミッドの骨格である。

はペンタトープグラフから2辺を削除して得られるグラフの一つで、もう一つは家Xグラフ。

輪グラフは潔い（Frucht 1979)。

車輪グラフはではグラフ次元2（つまり単位距離）、それ以外では次元3（つまり単位距離ではない）(Erdős et al. 1965, Buckley and Harary 1988).

任意の車輪グラフは自己双対グラフとなる.

Wolfram Languageで車輪グラフの作成はWheelGraphでできる.Wheel GraphはWhiteGraphで作成できる。

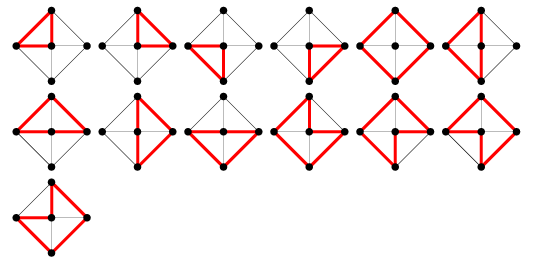
ホイールグラフのグラフサイクルの数はで与えられ、7, 13, 21, 31, 43, 57, …である。 (OEIS A002061) for , 5, …

車輪グラフにおいて、ハブは次数、他のノードは次数3。 車輪グラフは3-連結である。 ここで、は次数4の完全グラフ。 の色数は

(1)

であり、このグラフを見ると ホイールグラフ は色度多項式

(2)

となる。