ロジスティック回帰は、バイナリロジット、バイナリロジスティック回帰とも呼ばれ、特に有用な予測モデリング手法であります。 これは、例えば投票したかしなかったかといった2つのオプションを含む結果を予測するために使用されます。 以下では、解釈のために重みを使用するときの重みの意味だけを説明しようとします。

ロジスティック回帰での重みの解釈は、線形回帰での重みの解釈とは異なります。 重み付き和は、ロジスティック関数によって確率に変換される。

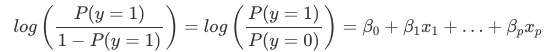
log()関数の項を「オッズ」（イベントの確率をイベントがない確率で割ったもの）と呼び、それを対数で包んだものを「ログオッズ」と呼ぶ。

この式からロジスティック回帰モデルはログオッズの線形モデルであることがわかる。 素晴らしい! 参考にならなそうですね! 少し項を入れ替えると、特徴量xjxjの1つを1単位変えたときに予測値がどう変わるかがわかります。 これを行うには、まず方程式の両辺に exp() 関数を適用します:

そして、特徴の値を 1 つ増やすとどうなるかを比較します。 ただし、差を見るのではなく、2つの予測値の比率を見ます：

以下のルールを適用します。

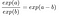
そして、多くの項を削除：

最後に、特徴重量の指数（）と同じくらい単純なものが出来上がる。 特徴が1単位変わると、exp(βj)exp(βj)の倍率でオッズ比（乗法）が変化するのです。 また、このように解釈することもできます。 xjxjが1単位変化すると、対応する重みの値だけ対数オッズ比が増加する。 多くの人がオッズ比を解釈するのは、何かの対数()を考えるのは脳に負担がかかると言われているからです。 オッズ比の解釈には、すでに慣れが必要です。 例えば、オッズが2であれば、y=1の確率がy=0の確率の2倍であることを意味し、重み（＝logオッズ比）が0.7であれば、それぞれの特徴を1単位増やすと、オッズはexp(0.7)（およそ2）倍になり4となる。しかし、通常はオッズは扱わず、重みはオッズ比としてのみ解釈されます。 なぜなら、実際にオッズを計算するためには、各特徴に値を設定する必要があり、それはデータセットの1つの特定のインスタンスを見たい場合にのみ意味があるからです。

These are the interpretations for the logistic regression model with different feature types:

• Numerical feature.これは、異なる特徴のタイプでロジスティック回帰モデルを解釈するためのものです。 特徴量xjxjの値を1単位増やすと、推定オッズはexp(βj)の倍数で変化する
• Binary categorical feature: 特徴量の2つの値のうち1つが参照カテゴリ（言語によっては0に符号化されたもの）である。 特徴量xjxjを基準カテゴリーからもう一方のカテゴリーに変更すると、推定オッズがexp(βj)exp(βj)のファクターで変化する。
• 2つ以上のカテゴリーを持つカテゴリー的特徴量。 複数のカテゴリーに対処する一つの解決策は、ワンホットエンコーディング、つまり各カテゴリーがそれ自身のカラムを持つことである。 L個のカテゴリを持つカテゴリ素性に対してL-1個の列があればよく、そうでなければ過剰なパラメータ化になってしまいます。 L番目のカテゴリは，参照カテゴリとなる． 線形回帰で使用できる他の任意のエンコーディングを使用することができる．
• Intercept β0β0: すべての数値特徴がゼロで、カテゴリ特徴が基準カテゴリにあるとき、推定オッズは exp(β0)exp(β0) となる。 切片重みの解釈は通常関係ない。