Programmation essentielle | Structures de contrôle
Boucles
Les « instructions de boucles » ne sont rien d’autre que l’automatisation de processus à plusieurs étapes en organisant des séquences d’actions, et en regroupant les parties qui doivent être répétées. Également un élément central de la programmation, l’itération (ou Looping) donne aux ordinateurs une grande partie de leur puissance. Ils peuvent répéter une séquence d’étapes aussi souvent que nécessaire, et des répétitions appropriées d’étapes simples peuvent résoudre des problèmes complexes.
En termes généraux, il existe deux types de « techniques de Looping »:
- « For Loops » : sont ceux qui s’exécutent pour un nombre prescrit de fois, comme contrôlé par un compteur ou un indice.
- « While Loops » et « Repeat Loops » : sont basés sur l’apparition et la vérification d’une condition logique. La condition est testée au début ou à la fin de la construction de la boucle.
Regardons-les :
1) Boucles For
Dans cette structure de contrôle, les déclarations sont exécutées l’une après l’autre dans un ordre consécutif sur une séquence de valeurs qui est évaluée uniquement lorsque la « boucle For » est initiée (jamais réévaluée). Dans ce cas, le nombre d’itérations est fixé et connu à l’avance.
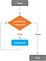
Si l’évaluation de la condition sur une variable (qui peut prendre des valeurs dans une séquence spécifiée) résulte VRAIE, une ou plusieurs déclarations seront exécutées séquentiellement sur cette chaîne de valeurs. Une fois que le premier test de condition est effectué (et que le résultat est VRAI), l’instruction est exécutée et la condition est évaluée à nouveau, selon un processus itératif. La partie « variable en séquence » effectue ce test sur chaque valeur de la séquence jusqu’à ce qu’elle couvre le dernier élément.
Si la condition n’est pas remplie et que le résultat est FAUX (par exemple, la partie « variable en séquence » a fini de parcourir tous les éléments de la séquence), la boucle se termine. Si le test de condition donne un résultat FAUX à la première itération, la « boucle For » n’est jamais exécutée.
La syntaxe des « For Loops » est:

Exemple 1
Pour montrer comment fonctionnent les « For Loops », nous allons d’abord créer une séquence en concaténant différents noms de fruits pour créer une liste (appelée « fruit_list ») :

Nous utiliserons cette liste de fruits comme « séquence » dans un « For Loop », et ferons en sorte que le « For Loop » exécute une instruction une fois (en imprimant le nom de chaque valeur) pour chaque valeur fournie dans la séquence (les différents fruits de la liste de fruits) :

De cette façon, le résultat du « For Loop » est le suivant:
## "Apple"
## "Kiwi"
## "Orange"
## "Banana"
OK, donc nous avons imprimé le nom de chaque valeur dans la liste. Pas grand-chose, n’est-ce pas ? La bonne nouvelle est que les « For Loops » peuvent être utilisés pour produire des résultats plus intéressants. Jetez un coup d’œil à l’exemple suivant.
Exemple 2
Que faire si nous voulons modifier des valeurs, ou effectuer des calculs de manière séquentielle ? Vous pouvez utiliser les « For Loops » pour effectuer des opérations mathématiques de manière séquentielle sur chaque valeur d’un vecteur (éléments de même type, qui dans ce cas seront numériques).
Dans cet exemple, nous allons créer une séquence de nombres (de 1 à 10), et définir une « Boucle For » pour calculer et imprimer la racine carrée de chaque valeur de cette séquence :

Dans ce cas, le résultat de la « Boucle For » est :
1
1.414214
1.732051
2
2.236068
2.449490
2.645751
2.828427
3
3.162278
Vous pouvez utiliser n’importe quel type d’opérateur mathématique sur une séquence numérique, et comme nous le verrons plus loin dans cet article, faire toutes sortes de combinaisons entre différentes structures de contrôle pour atteindre des résultats plus complexes.
2) Boucles While
Dans les « boucles While », une condition est d’abord évaluée, et si le résultat du test de cette condition est VRAI, une ou plusieurs déclarations sont exécutées de manière répétée jusqu’à ce que cette condition devienne FAUX.
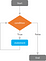
À la différence des « déclarations If », dans lesquelles une condition testée comme VRAIE exécute une expression une seule fois et se termine, les « While Loops » sont des déclarations itératives qui exécutent une certaine expression encore et encore jusqu’à ce que la condition devienne FAUX. Si la condition ne devient jamais FAUX, la boucle « While Loop » se poursuivra indéfiniment et le programme se plantera. Dans l’autre sens, si le test de la condition résulte FAUX au début de la boucle, l’expression ne sera jamais exécutée.
La syntaxe des « While Loops » est:

Exemple 1
Voyons un exemple. Tout d’abord, nous allons créer une variable (x) et lui attribuer la valeur 1. Ensuite, nous définissons une « boucle While » pour tester itérativement une condition sur cette variable jusqu’à ce que le test de la condition donne un résultat FAUX :

Voici comment cela fonctionne : la valeur initiale de la variable (x) est 1, donc lorsque nous testons la condition » la variable (x) est-elle inférieure à 10 ? », le résultat évalue à VRAI et l’expression est exécutée, imprimant le résultat de la variable (x), qui dans le premier cas est 1. Mais ensuite, il se passe quelque chose : la variable (x) est incrémentée de 1 avant que la fonction ne se termine, et à l’itération suivante, la valeur de x sera 2.
Cette réaffectation de variable est importante car elle finira par atteindre la condition FALSE et la sortie de boucle (valeur de x = 10). Le fait de ne pas modifier les conditions initiales dans une « boucle While » entraînera une boucle infinie et un plantage du programme.
Sortie
1
2
3
4
5
6
7
8
9
Exemple 2
Avez-vous entendu parler de la suite de Fibonacci ? Il s’agit d’une série de nombres ayant pour caractéristique que le prochain nombre de la séquence se trouve en additionnant les deux nombres qui le précèdent : 0, 1, 1, 2, 3, 5, 8, 13, 21,… Cette suite se retrouve dans plusieurs phénomènes de la nature, et a différentes applications en finance, en musique, en architecture, et dans d’autres disciplines.
Calculons-la en utilisant une « boucle While ».

Dans ce cas, nous fixons une valeur maximale dans la série comme condition d’arrêt, de sorte que la boucle imprime la série de Fibonacci uniquement pour les nombres inférieurs à 100. Quand un élément de la série (quel qu’il soit) devient plus grand que 100, le cycle de la boucle se termine.
0
1
1
2
3
5
8
13
21
34
55
89
Exemple 3
Une autre façon de générer la série de Fibonacci avec un « While Loop » est, au lieu de définir la valeur maximale de la série comme condition d’arrêt, de définir le nombre d’éléments de la série que vous voulez générer.

Ce « While Loop » ajoute l’élément suivant de la série à la fin de l’élément précédent, jusqu’à atteindre une condition d’arrêt. Dans ce cas, lorsque la série atteint 10 éléments (quelles que soient les valeurs), la boucle cylce se termine.
Sortie
0 1 1 2 3 5 8 13 21 34
3) Boucles de répétition
étroitement liées aux « boucles While », les « boucles de répétition » exécutent des déclarations de manière itérative, mais jusqu’à ce qu’une condition d’arrêt soit remplie. De cette façon, les déclarations sont exécutées au moins une fois, quel que soit le résultat de la condition, et la boucle ne sort que lorsque certaines conditions deviennent VRAIES :
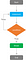
La syntaxe des « boucles de répétition » est :

Les « boucles répétées » utilisent des « déclarations de rupture » comme condition d’arrêt. « Les déclarations de rupture » sont combinées avec le test d’une condition pour interrompre les cycles à l’intérieur des boucles, puisque lorsque le programme frappe une rupture, il passera le contrôle à l’instruction immédiatement après la fin de la boucle (s’il y en a une).
Les « boucles répétées » s’exécuteront indéfiniment si la condition de rupture n’est pas remplie. Voyez ces 2 exemples
Exemple 1
D’abord nous créons une variable (x) et lui attribuons la valeur de 5. Ensuite, nous définissons une « boucle de répétition » pour imprimer itérativement la valeur de la variable, modifier la valeur de la variable (l’augmenter de 1) et tester une condition sur cette variable (si elle est égale à 10) jusqu’à ce que le résultat du test de condition soit VRAI.

La « condition de rupture » se déclenche lorsque la variable (x) atteint 10, et la boucle se termine.
Sortie
5
6
7
8
9
Exemple 2
Supposons maintenant que nous produisions une liste de nombres aléatoires, dont nous ne connaissons pas l’ordre ou la séquence de génération.
Dans cet exemple, nous utiliserons une « boucle de répétition » pour générer une séquence de nombres aléatoires normalement distribués (vous pouvez générer de l’aléatoire avec n’importe quelle autre distribution, nous choisissons simplement celle-ci), et rompre la séquence dès qu’un de ces nombres est supérieur à 1. Comme nous ne savons pas quels nombres viendront en premier, nous ne savons pas quelle sera la longueur de la séquence : nous connaissons juste la condition de rupture.

D’abord, nous utilisons l’instruction « set.seed » pour fixer les nombres aléatoires (générer toujours les mêmes nombres aléatoires), et rendre cet exemple reproductible.
Puis nous lançons la « boucle de répétition » en générant un nombre aléatoire normalement distribué, en l’imprimant, et en vérifiant si ce nombre est supérieur à 1. Ce n’est que lorsque cette condition devient VRAIE (cela peut être avec le premier nombre généré, ou non), que le cycle de la boucle passera à l’instruction break et se terminera.
Sortie
-0.9619334
-0.2925257
0.2587882
-1.152132
0.1957828
0.03012394
0.08541773
1.11661
Cela montre une fois de plus l’importance de fixer une condition de rupture appropriée. Ne pas le faire résultera en une boucle infinie.
Pensées finales
Nous avons vu et expliqué des concepts de manière isolée, mais les « structures de contrôle » peuvent être combinées comme vous le souhaitez : Les boucles peuvent contenir plusieurs boucles internes ; les conditionnels peuvent contenir des boucles et des conditionnels, les options sont infinies. (en fait, lors de l’examen de « Boucles répétées », nous avons constaté que les exemples contenaient des « déclarations If » imbriquées).
Vous pouvez développer des solutions avancées juste en combinant les « Structures de contrôle » que nous avons expliquées dans cet article. Comme l’a déclaré Minsky, nous pouvons atteindre des résultats complexes à la suite de l’interaction de composants plus simples. Les structures de contrôle constituent les blocs de base des processus décisionnels en informatique. Elles changent le flux des programmes et nous permettent de construire des ensembles complexes d’instructions à partir de blocs de construction plus simples.
Mon conseil est le suivant : apprenez à les connaître.
Cela facilitera votre chemin vers le codage et la compréhension des programmes, et vous aidera à trouver de nouvelles façons de résoudre les problèmes.