Comme défini dans cet ouvrage, un graphe de roue d’ordre , parfois simplement appelé une -roue (Harary 1994, p. 46 ; Pemmaraju et Skiena 2003, p. 248 ; Tutte 2005, p. 78), est un graphe qui contient un cycle d’ordre et pour lequel chaque sommet du graphe dans le cycle est connecté à un autre sommet du graphe appelé le moyeu. Les arêtes d’une roue qui incluent le moyeu sont appelées rayons (Skiena 1990, p. 146). La roue peut être définie comme la jointure de graphes , où est le graphe singleton et est le graphe cycle, ce qui en fait un graphe -cône.

Notez qu’il existe deux conventions pour l’indexation des graphes roue, certains auteurs (par ex, Gallian 2007), adoptant la convention selon laquelle désigne le graphe de roue sur nœuds.

Le graphe tétraédrique (c’est-à-dire ) est isomorphe à , et est isomorphe au graphe tripartite complet . En général, le graphe -roue est le squelette d’une -pyramide.

est l’un des deux graphes obtenus en retirant deux arêtes du graphe pentatope , l’autre étant le graphe maison X.

Les graphes-roues sont gracieux (Frucht 1979).

Le graphe à roue a une dimension de graphe 2 pour (et donc est à distance unitaire) et une dimension 3 sinon (et donc pas à distance unitaire) (Erdős et al. 1965, Buckley et Harary 1988).

Tout graphe à roue est un graphe auto-duel.

Les graphes à roue peuvent être construits dans le langage Wolfram en utilisant WheelGraph. Des propriétés précalculées d’un certain nombre de graphes de roue sont disponibles via GraphData.

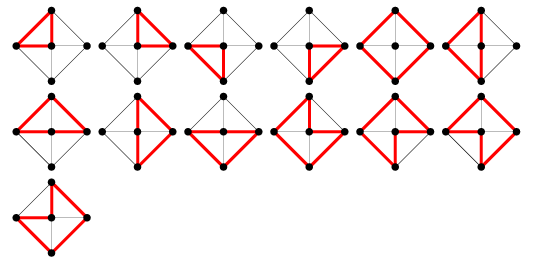
Le nombre de cycles du graphe de roue est donné par , ou 7, 13, 21, 31, 43, 57, …. (OEIS A002061) pour , 5, ….

Dans un graphe de roue, le moyeu a un degré , et les autres nœuds ont un degré 3. Les graphes de roue sont à 3 connexions. , où est le graphe complet d’ordre quatre. Le nombre chromatique de est

(1)

Le graphe roue a un polynôme chromatique

(2)

.