GeeksforGeeks
La méthode de la somme pondérée est une méthode de prise de décision multicritères dans laquelle il y aura plusieurs alternatives et nous devons déterminer la meilleure alternative en fonction de plusieurs critères. Il existe d’autres méthodes, notamment la méthode du produit pondéré (MPP), la technique d’ordre de préférence par similitude à la solution idéale (TOPSIS), VIKOR, MOORA, GTMA, etc. Comprenons le fonctionnement de la méthode des sommes pondérées à l’aide d’un exemple.
Considérez un cas où nous devons sélectionner le meilleur candidat parmi 5 candidats qui se présentent à un entretien. Le tableau 1 se compose des détails de 5 étudiants qui comprennent leur CGPA, le salaire qu’ils attendent par mois, leurs scores à l’examen technique et les notes obtenues par eux dans le test d’aptitude.
Tableau 1 : Exemple d’ensemble de données
| Attribut | CGPA | Salaire attendu | Score à l’examen technique | Test d’aptitude. Note |
|---|---|---|---|---|
| Étudiant 1 | 9 | 12000 | 72 | B1 |
| Étudiant 2 | 7.6 | 8500 | 68 | B1 |
| Etudiant 3 | 8.2 | 9500 | 63 | B2 |
| Etudiant 4 | 8.5 | 10000 | 70 | A2 |
| Etudiant 5 | 9.3 | 14000 | 72 | A2 |
Considérons les pondérations assumées par le jury d’entrevue comme suit :
CGPA = 30%, Allocation attendue = 20%, Note d’examen technique = 25%, Note d’examen d’aptitute = 25%
Tableau 2 : Les poids de chaque attribut
| Attribut | CGPA | Salaire attendu | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0.2 | 0.25 | 0.25 |
| Etudiant 1 | 9 | 12000 | 72 | B1 |
| Etudiant 2 | 7.6 | 8500 | 68 | B1 |
| Etudiant 3 | 8.2 | 9500 | 63 | B2 |
| Etudiant 4 | 8.5 | 10000 | 70 | A2 |
| Etudiant 5 | 9.3 | 14000 | 72 | A2 |
L’attribut bénéfique est celui dans lequel la personne désire des valeurs maximales. Ici, le CGPA, le score à l’examen technique et les scores au test d’aptitude sont des attributs bénéfiques car l’entreprise s’attend à ce que les étudiants aient plus de ces attributs.
L’attribut non bénéfique est celui dans lequel des valeurs minimales sont souhaitées. Dans ce cas, l’allocation attendue est un attribut non bénéfique. La société accroche les personnes qui sont prêtes à travailler plus avec un faible stipend.
Maintenant, voyons quel étudiant doit être sélectionné par la société en utilisant la méthode de la somme pondérée.
Pour cela, nous devons normaliser les valeurs du tableau 2.
- Pour les attributs bénéfiques,
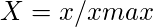
- Pour les attributs non bénéfiques,
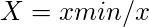
Tableau 3 : Décider de la valeur maximale pour un attribut bénéfique et de la valeur minimale pour un attribut non bénéfique
| Attribut | CGPA | Salaire attendu | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0.2 | 0.25 | 0.25 |
| Etudiant 1 | 9 | 12000 | 72(max) | B1 |
| Etudiant 2 | 7.6 | 8500(min) | 68 | B1 |
| Etudiant 3 | 8.2 | 9500 | 63 | B2 |
| Etudiant 4 | 8.5 | 10000 | 70 | A2(max) |
| Etudiant 5 | 9.3(max) | 14000 | 72 | A2 |
Nous considérerons les points suivants pour le système de notes
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tableau 4 : Mise à jour des notes du test d’aptitude
| Attribut | CGPA | Salaire prévu | Score à l’examen technique | Note du test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0.2 | 0.25 | 0.25 |
| Etudiant 1 | 9 | 12000 | 72(max) | 3 |
| Etudiant 2 | 7.6 | 8500(min) | 68 | 3 |
| Elève 3 | 8.2 | 9500 | 63 | 2 |
| Elève 4 | 8.5 | 10000 | 70 | 4(max) |
| Etudiant 5 | 9.3(max) | 14000 | 72 | 4 |
Normaliser les valeurs de l’attribut respectif en fonction de l’attribut bénéfique et non bénéfique.
Tableau 5 : Normalisation
| Attribut | CGPA | Salaire attendu | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0,2 | 0,25 | 0,25 |
| Élève 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Etudiant 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Etudiant 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Etudiant 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Etudiant 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tableau 6 : La matrice de décision normalisée par le poids
| Attribut | CGPA | Subvention attendue | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0,2 | 0,25 | 0,25 |
| Elève 1 | 0,9677 | 0,7083 | 1 | 0.75 |
| Étudiant 2 | 0,8172 | 1 | 0,9444 | 0,75 |
| Étudiant 3 | 0,8817 | 0,8947 | 0.875 | 0,5 |
| Elève 4 | 0,9134 | 0,85 | 0,9722 | 1 |
| Elève 5 | 1 | 0.6071 | 1 | 1 |
Tableau 7 : Multiplication de chaque paramètre par les poids respectifs
| Attribut | CGPA | Salaire prévu | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0,2 | 0,25 | 0,25 |
| Élève 1 | 0,9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Élève 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Élève 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Élève 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0,25 |
| Élève 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
Le tableau ci-dessus est simplifié comme suit
Tableau 8 : Version simplifiée du tableau 7
| Attribut | CGPA | Salaire prévu | Score à l’examen technique | Note au test d’aptitude |
|---|---|---|---|---|
| Poids | 0.3 | 0,2 | 0,25 | 0,25 |
| Élève 1 | 0.29031 | 0,14166 | 0,25 | 0,1875 |
| Élève 2 | 0.24516 | 0,2 | 0,2361 | 0,1875 |
| Élève 3 | 0,26451 | 0.17894 | 0,21875 | 0,125 |
| Élève 4 | 0,27402 | 0,17 | 0.24305 | 0,25 |
| Elève 5 | 0,3 | 0,12142 | 0,25 | 0.25 |
Il faut additionner les composantes de chaque ligne et calculer la somme pondérée qui est la note de performance et donner les priorités aux élèves
Tableau 9 : Calcul du rang des rangs des étudiants par score de performance
| Attribut | CGPA | Salaire attendu | Score à l’examen technique | Note au test d’aptitude | Score de performance | Rang |
|---|---|---|---|---|---|---|
| Poids | 0.3 | 0,2 | 0,25 | 0,25 | ||
| Elève 1 | 0,29031 | 0,14166 | 0,25 | 0,1875 | 0.86947 | 3 |
| Etudiant 2 | 0,24516 | 0,2 | 0,2361 | 0.1875 | 0,86876 | 4 |
| Étudiant 3 | 0,26451 | 0.17894 | 0,21875 | 0,125 | 0,7872 | 5 |
| Élève 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Etudiant 5 | 0.3 | 0.12142 | 0.25 | 0,25 | 0,92142 | 2 |
Conclusion : A partir de la méthode de la somme pondérée, il est décidé que l’élève 4 est le meilleur choix parmi les autres.