Comment interpréter les poids dans la régression logistique
La régression logistique, également appelée logit binaire et régression logistique binaire, est une technique de modélisation prédictive particulièrement utile. Elle est utilisée pour prédire les résultats impliquant deux options, que vous ayez voté ou non par exemple. Ci-dessous, je vais essayer d’expliquer simplement ce que signifient les poids lorsque vous les utilisez pour des interprétations.
L’interprétation des poids dans la régression logistique diffère de l’interprétation des poids dans la régression linéaire, puisque le résultat dans la régression logistique est une probabilité entre 0 et 1. Les poids n’influencent plus la probabilité de façon linéaire. La somme pondérée est transformée par la fonction logistique en une probabilité. Nous devons donc reformuler l’équation de l’interprétation pour que seul le terme linéaire soit du côté droit de la formule.
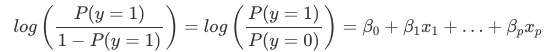
Nous appelons le terme de la fonction log() « odds » (probabilité de l’événement divisée par la probabilité de l’absence d’événement) et enveloppé dans le logarithme, il est appelé log odds.
Cette formule montre que le modèle de régression logistique est un modèle linéaire pour le log odds. Génial ! Cela ne semble pas utile ! En mélangeant un peu les termes, vous pouvez déterminer comment la prédiction change lorsqu’une des caractéristiques xjxj est modifiée d’une unité. Pour ce faire, nous pouvons d’abord appliquer la fonction exp() aux deux côtés de l’équation :

Puis nous comparons ce qui se passe lorsque nous augmentons la valeur d’une des caractéristiques de 1. Mais au lieu de regarder la différence, nous regardons le rapport des deux prédictions :

Nous appliquons la règle suivante :
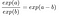
Et nous supprimons de nombreux termes :

A la fin, nous avons quelque chose d’aussi simple que exp() d’un poids de caractéristique. Un changement d’une unité dans une caractéristique change l’odds ratio (multiplicatif) par un facteur de exp(βj)exp(βj). On peut aussi l’interpréter de la façon suivante : Un changement dans xjxj d’une unité augmente l’odds ratio logarithmique de la valeur du poids correspondant. La plupart des gens interprètent le rapport de cotes parce que penser au log() de quelque chose est connu pour être difficile pour le cerveau. Il faut déjà s’habituer à interpréter le rapport de cotes. Par exemple, si vous avez une probabilité de 2, cela signifie que la probabilité de y=1 est deux fois plus élevée que celle de y=0. Si vous avez un poids (= logarithme du rapport de cotes) de 0,7, alors le fait d’augmenter la caractéristique respective d’une unité multiplie les cotes par exp(0,7) (environ 2) et les cotes passent à 4. Mais généralement, vous ne vous occupez pas des cotes et vous interprétez les poids uniquement comme des rapports de cotes. Parce que pour calculer réellement les cotes, vous auriez besoin de définir une valeur pour chaque caractéristique, ce qui n’a de sens que si vous voulez examiner une instance spécifique de votre ensemble de données.
Voici les interprétations pour le modèle de régression logistique avec différents types de caractéristiques:
- Caractère numérique : Si vous augmentez la valeur de la caractéristique xjxj d’une unité, les chances estimées changent par un facteur de exp(βj)exp(βj)
- Catégorique binaire : L’une des deux valeurs de la caractéristique est la catégorie de référence (dans certaines langues, celle codée en 0). Le changement de la caractéristique xjxj de la catégorie de référence à l’autre catégorie change la cote estimée par un facteur de exp(βj)exp(βj).
- Caractéristique catégorielle avec plus de deux catégories : Une solution pour traiter les catégories multiples est le codage à un coup, ce qui signifie que chaque catégorie a sa propre colonne. Vous n’avez besoin que de L-1 colonnes pour une caractéristique catégorielle avec L catégories, sinon elle est sur-paramétrée. La L-ième catégorie est alors la catégorie de référence. Vous pouvez utiliser n’importe quel autre encodage qui peut être utilisé dans la régression linéaire. L’interprétation pour chaque catégorie est alors équivalente à l’interprétation des caractéristiques binaires.
- Intercept β0β0 : Lorsque toutes les caractéristiques numériques sont nulles et que les caractéristiques catégorielles sont à la catégorie de référence, les chances estimées sont exp(β0)exp(β0). L’interprétation du poids de l’ordonnée à l’origine n’est généralement pas pertinente.