Como se define en este trabajo, un gráfico de rueda de orden , a veces llamado simplemente una rueda (Harary 1994, p. 46; Pemmaraju y Skiena 2003, p. 248; Tutte 2005, p. 78), es un grafo que contiene un ciclo de orden y para el cual cada vértice del grafo en el ciclo está conectado a otro vértice del grafo conocido como el centro. Las aristas de una rueda que incluyen el cubo se llaman radios (Skiena 1990, p. 146). La rueda puede definirse como la unión de grafos , donde es el grafo singleton y es el grafo del ciclo, lo que lo convierte en un grafo -cono.

Nótese que hay dos convenciones para la indexación de los grafos de rueda, con algunos autores (por ejemplo, Gallian 2007), adoptando la convención de que denota el gráfico de la rueda en nodos.

El gráfico tetraédrico (es decir, ) es isomorfo a , y es isomorfo al gráfico tripartito completo . En general, el grafo -rueda es el esqueleto de una -pirámide.

es uno de los dos grafos que se obtienen al eliminar dos aristas del grafo pentatopo , siendo el otro el grafo de la casa X.

Los grafos de rueda son graciosos (Frucht 1979).

El grafo de la rueda tiene dimensión gráfica 2 para (y por lo tanto es de distancia unitaria) y dimensión 3 en caso contrario (y por lo tanto no es de distancia unitaria) (Erdős et al. 1965, Buckley y Harary 1988).

Cualquier grafo de la rueda es un grafo autodual.

Los grafos de la rueda se pueden construir en Wolfram Language utilizando WheelGraph. Las propiedades precalculadas de un número de grafos de rueda están disponibles a través de GraphData.

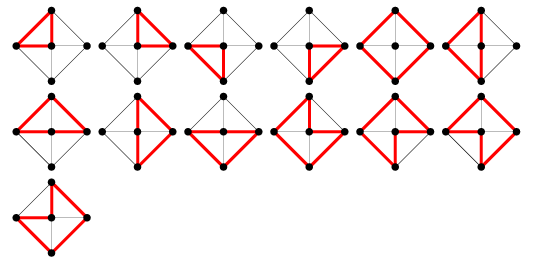
El número de ciclos del grafo está dado por , o 7, 13, 21, 31, 43, 57, … (OEIS A002061) para , 5, ….

En un grafo de rueda, el cubo tiene grado , y otros nodos tienen grado 3. Los grafos de rueda están conectados por 3. , donde es el grafo completo de orden cuatro. El número cromático de es

(1)

El gráfico de la rueda tiene polinomio cromático

(2)