GeeksforGeeks
El método de la suma ponderada es un método de toma de decisiones multicriterio en el que habrá múltiples alternativas y tenemos que determinar la mejor alternativa en base a múltiples criterios. Existen otros métodos como el Método del Producto Ponderado (WPM), la Técnica de Orden de Preferencia por Similitud a la Solución Ideal (TOPSIS), VIKOR, MOORA, GTMA, etc. Vamos a entender el funcionamiento del Método de la Suma Ponderada con un ejemplo.
Consideremos un caso en el que tenemos que seleccionar al mejor candidato entre 5 candidatos que se presentan a una entrevista. La tabla 1 consta de los datos de 5 estudiantes que incluyen su CGPA, el salario que esperan al mes, sus puntuaciones en el examen técnico y las calificaciones obtenidas por ellos en la prueba de aptitud.
Tabla 1: Conjunto de datos de muestra
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Prueba de aptitud Grado |
|---|---|---|---|---|
| Estudiante 1 | 9 | 12000 | 72 | B1 |
| Estudiante 2 | 7.6 | 8500 | 68 | B1 |
| Estudiante 3 | 8.2 | 9500 | 63 | B2 |
| Estudiante 4 | 8,5 | 10000 | 70 | A2 |
| Estudiante 5 | 9.3 | 14000 | 72 | A2 |
Considere las ponderaciones asumidas por el panel entrevistador de la siguiente manera :
CGPA = 30%, Estipendio esperado = 20%, Puntuación del examen técnico = 25%, Nota del examen de aptitud = 25%
Tabla 2: Los pesos de cada atributo
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Calificación en la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Estudiante 1 | 9 | 12000 | 72 | B1 |
| Estudiante 2 | 7.6 | 8500 | 68 | B1 |
| Estudiante 3 | 8.2 | 9500 | 63 | B2 |
| Estudiante 4 | 8,5 | 10000 | 70 | A2 |
| Estudiante 5 | 9.3 | 14000 | 72 | A2 |
Atributo beneficioso es aquel en el que la persona desea los máximos valores. En este caso, el CGPA, la puntuación del examen técnico y las puntuaciones de la prueba de aptitud son atributos beneficiosos, ya que la empresa espera que los estudiantes tengan más de estos atributos.
Atributo no beneficioso es aquel en el que se desean valores mínimos. En este caso, el estipendio esperado es un atributo no beneficioso. La empresa sube a las personas que están dispuestas a trabajar más con un estipendio bajo.
Ahora vamos a ver qué estudiante va a ser seleccionado por la empresa mediante el método de la suma ponderada.
Para ello, debemos normalizar los valores de la tabla 2.
- Para los atributos beneficiosos,
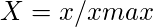
- Para los no beneficiosos,
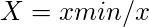
Tabla 3: Decidir el valor máximo para un atributo beneficioso y el valor mínimo para un atributo no beneficioso
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Calificación en la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Estudiante 1 | 9 | 12000 | 72(máx) | B1 |
| Estudiante 2 | 7.6 | 8500(min) | 68 | B1 |
| Estudiante 3 | 8.2 | 9500 | 63 | B2 |
| Estudiante 4 | 8.5 | 10000 | 70 | A2(max) |
| Estudiante 5 | 9.3(max) | 14000 | 72 | A2 |
Consideraremos los siguientes puntos para el sistema de calificaciones
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabla 4: Actualización de las calificaciones de la prueba de aptitud
| Atributo | CGPA | Estipendio esperado | Puntuación del examen técnico | Calificación de la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Estudiante 1 | 9 | 12000 | 72(máx) | 3 |
| Estudiante 2 | 7.6 | 8500(min) | 68 | 3 |
| Estudiante 3 | 8,2 | 9500 | 63 | 2 |
| Estudiante 4 | 8.5 | 10000 | 70 | 4(max) |
| Estudiante 5 | 9.3(max) | 14000 | 72 | 4 |
Normaliza los valores del atributo respectivo en función del atributo beneficioso y no beneficioso.
Tabla 5: Normalización
| Atributo | CGPA | Estipendio esperado | Puntuación del examen técnico | Calificación de la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0,2 | 0,25 | 0,25 |
| Estudiante 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Estudiante 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Estudiante 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Estudiante 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Estudiante 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabla 6: La matriz de decisión normalizada por peso
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Calificación en la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0,2 | 0,25 | 0,25 |
| Estudiante 1 | 0,9677 | 0,7083 | 1 | 0.75 |
| Estudiante 2 | 0,8172 | 1 | 0,9444 | 0,75 |
| Estudiante 3 | 0,8817 | 0,8947 | 0.875 | 0,5 |
| Estudiante 4 | 0,9134 | 0,85 | 0,9722 | 1 |
| Estudiante 5 | 1 | 0.6071 | 1 | 1 |
Tabla 7: Multiplicando cada parámetro con los respectivos pesos
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Calificación en la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0,2 | 0,25 | 0,25 |
| Estudiante 1 | 0,9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Estudiante 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Estudiante 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Estudiante 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0,25 |
| Estudiante 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
La tabla anterior se simplifica como sigue
Tabla 8: Versión simplificada de la tabla 7
| Atributo | CGPA | Estipendio esperado | Puntuación del examen técnico | Calificación de la prueba de aptitud |
|---|---|---|---|---|
| Peso | 0.3 | 0,2 | 0,25 | 0,25 |
| Estudiante 1 | 0.29031 | 0,14166 | 0,25 | 0,1875 |
| Estudiante 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Estudiante 3 | 0.26451 | 0.17894 | 0,21875 | 0,125 |
| Estudiante 4 | 0,27402 | 0,17 | 0.24305 | 0,25 |
| Estudiante 5 | 0,3 | 0,12142 | 0,25 | 0.25 |
Hay que sumar los componentes de cada fila y calcular la suma ponderada que es la puntuación del rendimiento y dar las prioridades a los alumnos
Tabla 9: Cálculo de la clasificación de los rangos de los estudiantes según la puntuación de rendimiento
| Atributo | CGPA | Estipendio esperado | Puntuación en el examen técnico | Calificación en la prueba de aptitud | Puntuación en el rendimiento | Rango |
|---|---|---|---|---|---|---|
| Peso | 0.3 | 0,2 | 0,25 | 0,25 | ||
| Estudiante 1 | 0,29031 | 0,14166 | 0,25 | 0,1875 | 0.86947 | 3 |
| Estudiante 2 | 0,24516 | 0,2 | 0,2361 | 0.1875 | 0,86876 | 4 |
| Estudiante 3 | 0,26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Estudiante 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Estudiante 5 | 0,3 | 0,12142 | 0.25 | 0,25 | 0,92142 | 2 |
Conclusión : A partir del método de la suma ponderada, se decide que el alumno 4 es la mejor opción entre los demás.