Introducción

Recientemente hemos propuesto un mecanismo de recuperación de información asociativa que tiene en cuenta explícitamente las representaciones neuronales a largo plazo de los elementos de memoria (Romani et al., 2013). Una de las predicciones básicas del modelo es la existencia de palabras «fáciles» y «difíciles». Esta predicción se verificó en nuestro análisis de un gran conjunto de datos de experimentos de recuerdo libre recogidos en el laboratorio de Michael Kahana, donde demostramos que la probabilidad de que las palabras sean recordadas son consistentes entre grupos de sujetos elegidos arbitrariamente (Katkov et al., presentado). La pregunta natural que plantean estas observaciones es qué características son predictivas de la dificultad de las palabras en los experimentos de recuerdo, en particular cuál es la contribución de la longitud de la palabra, si es que hay alguna.

La mayoría de los estudios anteriores sobre el efecto de la longitud de la palabra utilizaron listas que estaban compuestas específicamente por palabras cortas o largas. En dos estudios anteriores en los que se utilizaron listas compuestas por palabras cortas y largas alternativamente, no se observó ningún efecto de la longitud de las palabras (Hulme et al., 2004; Jalbert et al., 2011). Nuestra contribución actual utiliza el paradigma de recuerdo libre y se basa en un conjunto de datos mucho mayor que el de los estudios anteriores. Informamos que cuando las palabras se seleccionan al azar, independientemente de su longitud, las palabras largas se recuerdan mejor que las cortas, en una aparente contradicción con el efecto clásico de la longitud de la palabra tanto en el recuerdo serial como en el libre (Baddeley et al., 1975; Russo y Grammatopoulou, 2003; Tehan y Tolan, 2007; Bhatarah et al., 2009). Proporcionamos una posible resolución de esta contradicción en el marco del modelo de recuperación asociativa de (Romani et al., 2013).

Materiales y métodos

Métodos experimentales

Los datos reportados en este manuscrito fueron recolectados en el laboratorio de M. Kahana como parte del Penn Electrophysiology of Encoding and Retrieval Study (ver Miller et al., 2012 para detalles de los experimentos). Aquí analizamos los resultados de los 141 participantes (de 17 a 30 años) que completaron la primera fase del experimento, que consistió en siete sesiones experimentales. Los participantes dieron su consentimiento según el protocolo del IRB de la Universidad de Pensilvania y fueron compensados por su participación. Cada sesión consistió en 16 listas de 16 palabras presentadas de una en una en la pantalla del ordenador y duró aproximadamente 1,5 h. Cada lista de estudio iba seguida de una prueba de recuerdo libre inmediato. Las palabras se extrajeron de un conjunto de 1638 palabras. Para cada lista, había un retraso de 1500 ms antes de que apareciera la primera palabra en la pantalla. Cada elemento estaba en la pantalla durante 3000 ms, seguido de un intervalo entre estímulos de 800-1200 ms (distribución uniforme). Después del último elemento de la lista, había un retraso de 1200-1400 ms, tras el cual el participante tenía 75 s para intentar recordar cualquiera de los elementos recién presentados. Se utilizaron todos los ensayos; se eliminaron las intrusiones y las repeticiones de los ensayos.

El modelo

Suponemos que cada palabra está representada por una población de neuronas elegida al azar en la red de memoria dedicada. Asumimos además que cada ítem recuperado actúa como una pista interna para el siguiente según la medida de similitud entre ítems, que se define como un el tamaño de la intersección entre las poblaciones correspondientes (el número de neuronas que representan ambos ítems). Siguiendo a (Romani et al., 2013), consideramos el proceso de recuperación que está directamente determinado por las representaciones de memoria de los ítems, sin simular explícitamente la actividad de la red. La dinámica de la recuperación se describe mediante una secuencia de elementos recordados. El primero se elige aleatoriamente entre los presentados, y cada elemento recordado posterior se elige para ser el que tiene una similitud máxima con el actualmente recordado, sin contar sólo el elemento «visitado» (Romani et al., 2013). La recuperación se termina cuando el proceso de recuperación entra en un ciclo y no se pueden recuperar más elementos.

Para imitar el protocolo experimental (véase más arriba), generamos W = 1638 patrones binarios aleatorios de longitud N: {ξiw = 0; 1} con w = 1, … , W; i = 1, … , N indica las neuronas en la red, tales que ξiw = 1 si la neurona i está participando en la codificación del elemento de memoria w. La similitud entre los elementos w y w′ se calcula entonces como Sww′=∑i=1Nξiwξiw′. Los componentes de los patrones para cada ítem se extrajeron de forma independiente con la probabilidad pw de ξiw = 1 elegida de la siguiente manera: a cada patrón se le asignó arbitrariamente una longitud silábica lw = 1…4 de tal forma que la distribución de lw a través de los patrones coincidiera con la distribución correspondiente a través de las palabras utilizadas en el experimento (cinco palabras con longitud silábica mayor a cuatro se combinaron con las de longitud cuatro). Para los patrones con una lw determinada, las pw correspondientes se distribuyeron de forma equidistante entre 0,02 – 10-3lw y 0,02 + 10-3lw. Con esta elección de las estadísticas de los patrones, el número medio de neuronas que representan un elemento dado no depende de su longitud silábica, mientras que la varianza aumenta con la longitud silábica. Las representaciones de las palabras se fijaron a lo largo del experimento simulado.

Para cada ensayo de recuerdo simulado, se eligieron L = 16 ítems para su presentación según dos protocolos experimentales. Para el primero, los ítems se seleccionaron de forma completamente independiente, como en el experimento de Kahana. Para el segundo protocolo, los ítems con el mismo lw se seleccionaron al azar. El proceso de recuerdo se simuló como en (Romani et al., 2013). El primer ítem recordado fue elegido al azar entre los presentados. Las transiciones posteriores entre los ítems recordados se determinaron mediante la matriz de similitud S entre ellos, cada elemento de la cual se calculó como el número de neuronas en la intersección entre las representaciones correspondientes: Sww′=∑i=1Nξiwξiw′. Más concretamente, el siguiente elemento recuperado es el que tiene la máxima similitud con el actual, excluyendo el elemento que se recuperó justo antes del actual. El recuerdo se termina cuando el proceso de recuperación entra en un ciclo y no se pueden recuperar más elementos.

Resultados

Analizamos un gran conjunto de datos de experimentos de recuerdo libre realizados por 141 sujetos con 112 ensayos por sujeto. Los datos se recogen en el laboratorio de Michael Kahana. Las listas estaban compuestas por 16 palabras seleccionadas al azar de un conjunto de 1638 palabras. Se utilizaron todos los ensayos; se eliminaron las intrusiones y las repeticiones de los ensayos (en total 15792 ensayos, véase la sección Métodos). Para cada palabra, se calculó su probabilidad global de recuerdo (Prec) como la fracción de ensayos en los que se recordó esta palabra cuando se presentó. La Figura 1 muestra la distribución de (Prec) para todas las palabras que tienen un número determinado de sílabas (en negro) agregadas de todos los ensayos. La distribución de Prec es amplia para todas las longitudes de las palabras. Sin embargo, la probabilidad media de recuerdo y su varianza crecen monótonamente con el número de sílabas (el coeficiente de correlación es 0,15, p < 10-6).

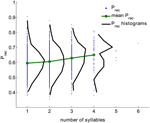
Figura 1. Probabilidad de recuerdo de palabras con diferente número de sílabas (puntos azules), la distribución de las probabilidades de recuerdo (negro) y el valor medio de la probabilidad de recuerdo (verde) calculado a partir de los datos experimentales. El coeficiente de correlación entre el número de sílabas y la probabilidad de recuerdo es de 0,15, p < 10-6).

Este resultado parece contradecir el efecto clásico de la longitud de las palabras, en el que se demostró que las listas de palabras cortas se recordaban mejor que las listas de palabras largas (Baddeley et al., 1975; Russo y Grammatopoulou, 2003; Tehan y Tolan, 2007; Bhatarah et al., 2009). Para comprobar si estos dos efectos pueden ser explicados por el mecanismo de recuperación que proponemos, simulamos el modelo imitando paradigmas experimentales en dos condiciones: recuerdo libre con listas compuestas de palabras cortas/largas y listas aleatorias (ver Métodos). El resultado fue sorprendente: el rendimiento en la tarea de recuerdo libre depende del paradigma experimental: en el recuerdo de una mezcla aleatoria de palabras no relacionadas, las palabras más largas son estadísticamente más fáciles de recordar, mientras que en las listas compuestas por palabras con un número fijo de sílabas, las palabras más cortas son más fáciles de recordar (Figura 2).

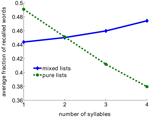
Figura 2. Fracción media de palabras recordadas en función del número de sílabas del modelo. Las listas puras se componen utilizando sólo palabras con el mismo número de sílabas. Las listas mixtas se componen de todo el conjunto de palabras.

La mayoría de las explicaciones de los efectos clásicos de la longitud de las palabras asumen que la longitud total de los estímulos presentados está correlacionada negativamente con el número de palabras recordadas. Para comprobar si esta afirmación está respaldada por los datos, calculamos la correlación entre el número de sílabas de las listas presentadas y el número de palabras recordadas. No encontramos prácticamente ninguna correlación (el coeficiente de correlación es 0,004 y no es significativamente diferente de 0, p = 0,67).

Discusión

El efecto de longitud de las palabras, es decir, la observación de que las listas de palabras cortas se recuerdan mejor que las listas de palabras largas (Baddeley et al., 1975) se considera uno de los fenómenos clave en las teorías de la memoria a corto plazo (Campoy, 2011; Jalbert et al., 2011). Aquí informamos de que en el recuerdo libre de palabras no relacionadas, donde se mezclan aleatoriamente palabras cortas y largas, las palabras largas tienen mayor probabilidad de recuerdo que las cortas, en aparente contradicción con el efecto de la longitud de la palabra.

El efecto clásico de la longitud de la palabra se explica tradicionalmente por una mayor complejidad de los elementos más largos (Neath y Nairne, 1995), o por un mayor tiempo de ensayo de los elementos más largos (Baddeley, 1986, 2003; Page y Norris, 1998; Burgess y Hitch, 1999). La primera explicación sugiere que las palabras más cortas son genéricamente más fáciles de recordar, lo que no es compatible con nuestra observación. En la segunda explicación, se pueden ensayar más palabras cortas, debido al menor tiempo de ensayo, y por tanto se recuerdan más. Esta explicación no especifica en qué orden se ensayarían las palabras presentadas, pero sugiere una correlación negativa entre la longitud total de los elementos presentados y el número de palabras recordadas, mientras que no existe tal correlación en los datos.

Aquí mostramos que nuestro mecanismo recientemente sugerido de recuperación asociativa puede explicar potencialmente tanto el efecto clásico de la longitud de las palabras (que también está presente en los experimentos de recuerdo libre, véase Russo y Grammatopoulou, 2003; Bhatarah et al., 2009) como el efecto opuesto de la longitud en las listas de palabras seleccionadas al azar reportado en esta contribución. A diferencia de los modelos existentes, la representación neuronal a largo plazo de los ítems juega un papel crucial en nuestro modelo, y no se requiere un mecanismo separado de memoria a corto plazo. En particular, la probabilidad de recordar elementos en listas aleatorias aumenta con el tamaño de su representación en relación con la de otros elementos, y estos elementos se recuerdan antes y suprimen los elementos con representaciones más pequeñas (Romani et al., 2013). Sin embargo, la probabilidad media de recuerdo de todo el conjunto de ítems es independiente del tamaño medio de la representación, pero se relaciona negativamente con la varianza del tamaño de la representación en todo el conjunto (Katkov et al., presentado). Por lo tanto, asumimos que las palabras más largas no tienen, de media, una mayor representación que las más cortas, sino que colectivamente tienen una mayor varianza del tamaño de la representación. Esta suposición no tiene actualmente una justificación biológica directa, pero nos permitió conciliar la aparente contradicción entre las observaciones experimentales. En particular, explica el efecto clásico de la longitud de la palabra, en el que sólo se presentan palabras con una longitud silábica determinada y, por tanto, la varianza del tamaño de la representación aumenta con la longitud silábica. En las listas con longitud silábica mixta, en algunos ensayos los elementos con mayor longitud silábica tienen mayor representación neuronal. Cuando se presentan estas listas, las palabras más largas tienen mayor probabilidad de ser recordadas, suprimiendo otros ítems de ser recordados, resultando en una leve correlación positiva entre la longitud silábica de un ítem y su probabilidad de recuerdo.

Los resultados presentados en esta contribución muestran que la longitud de la palabra es un factor prominente que afecta a la facilidad para ser recordada. Sin embargo, observamos que las probabilidades de recuerdo siguen mostrando una amplia distribución incluso para palabras de longitud determinada, lo que indica que otras características de la palabra, aún desconocidas, también contribuyen a la probabilidad de recordar una palabra.

Declaración de conflicto de intereses

Los autores declaran que la investigación se llevó a cabo en ausencia de cualquier relación comercial o financiera que pudiera interpretarse como un potencial conflicto de intereses.

Agradecimientos

Agradecemos a M. Kahana por compartir generosamente con nosotros los datos obtenidos en su laboratorio. El laboratorio de Kahana cuenta con el apoyo de la subvención MH55687 de los NIH. Misha Tsodyks cuenta con el apoyo del FP7 de la UE (acuerdo de subvención 604102), la Fundación Científica Israelí y la Fundación Adelis. Sandro Romani cuenta con el apoyo de una beca de larga duración del Human Frontier Science Program.