La regresión logística, también conocida como logit binario y regresión logística binaria, es una técnica de modelado predictivo particularmente útil. Se utiliza para predecir resultados que implican dos opciones, si ha votado o no ha votado, por ejemplo. A continuación trataré de explicar simplemente lo que significan los pesos cuando se utilizan para las interpretaciones.

La interpretación de los pesos en la regresión logística difiere de la interpretación de los pesos en la regresión lineal, ya que el resultado en la regresión logística es una probabilidad entre 0 y 1. Los pesos ya no influyen linealmente en la probabilidad. La suma ponderada es transformada por la función logística en una probabilidad. Por lo tanto, tenemos que reformular la ecuación para la interpretación de manera que sólo el término lineal esté en el lado derecho de la fórmula.

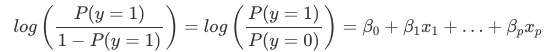
Llamamos al término de la función log() «probabilidades» (probabilidad del suceso dividida por la probabilidad de que no haya ningún suceso) y envuelto en el logaritmo se llama log probabilidades.

Esta fórmula muestra que el modelo de regresión logística es un modelo lineal para el log probabilidades. Genial. ¡Eso no parece útil! Con un poco de barajar los términos, se puede averiguar cómo cambia la predicción cuando una de las características xjxj se cambia en 1 unidad. Para ello, primero podemos aplicar la función exp() a ambos lados de la ecuación:

Entonces comparamos lo que ocurre cuando aumentamos en 1 uno de los valores de las características. Pero en lugar de mirar la diferencia, miramos el ratio de las dos predicciones:

Aplicamos la siguiente regla:

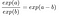
Y eliminamos muchos términos:

Al final, tenemos algo tan simple como exp() del peso de una característica. Un cambio en un rasgo en una unidad cambia el odds ratio (multiplicativo) en un factor de exp(βj)exp(βj). También podríamos interpretarlo de esta manera: Un cambio en xjxj en una unidad aumenta la log odds ratio en el valor del peso correspondiente. La mayoría de la gente interpreta el odds ratio porque se sabe que pensar en el log() de algo es difícil para el cerebro. Interpretar la razón de momios ya requiere acostumbrarse. Por ejemplo, si tiene probabilidades de 2, significa que la probabilidad de y=1 es dos veces mayor que la de y=0. Si tiene un peso (= logaritmo de la razón de probabilidades) de 0,7, entonces el aumento de la característica respectiva en una unidad multiplica las probabilidades por exp(0,7) (aproximadamente 2) y las probabilidades cambian a 4. Pero normalmente no se trata de las probabilidades y se interpretan los pesos sólo como las razones de probabilidades. Porque para calcular realmente las probabilidades tendría que establecer un valor para cada característica, lo que sólo tiene sentido si quiere mirar una instancia específica de su conjunto de datos.

Estas son las interpretaciones para el modelo de regresión logística con diferentes tipos de características:

• Característica numérica: Si se aumenta el valor del rasgo xjxj en una unidad, las probabilidades estimadas cambian en un factor de exp(βj)exp(βj)
• Característica categórica binaria: Uno de los dos valores del rasgo es la categoría de referencia (en algunos idiomas, la codificada en 0). El cambio del rasgo xjxj de la categoría de referencia a la otra categoría cambia las probabilidades estimadas por un factor de exp(βj)exp(βj).
• Característica categórica con más de dos categorías: Una solución para tratar con múltiples categorías es la codificación de un solo golpe, lo que significa que cada categoría tiene su propia columna. Sólo se necesitan L-1 columnas para una característica categórica con L categorías, de lo contrario se sobreparametriza. La L-ésima categoría es entonces la categoría de referencia. Se puede utilizar cualquier otra codificación que se pueda utilizar en la regresión lineal. La interpretación para cada categoría es entonces equivalente a la interpretación de las características binarias.
• Intercepto β0β0: Cuando todas las características numéricas son cero y las características categóricas están en la categoría de referencia, las probabilidades estimadas son exp(β0)exp(β0). La interpretación del peso del intercepto no suele ser relevante.